If you have ever been through High school, then you would know about the three main trigonometric functions: Sine, Cosine, and Tangent. For many people, these equations may appear relatively simple, but that is not always the case, especially with higher level sciences.
This is especially useful in fields like high-level physics where the answer can appear extremely complex and difficult to understand. To help with this, one can use small angle approximations. Small angle approximations allow you to substitute the trigonometric function for another value which is “good enough” to complete the calculation.
What are small angle approximations?
The small angle approximations for trigonometric functions are as follows: sin(x) = x, cos(x) = 1, and tan(x) = x where x is close to zero. As an angle approaches zero, these numbers become increasingly accurate, finally reaching an exact approximation when the number reaches zero. The actual error found in the calculations for each function are listed below:
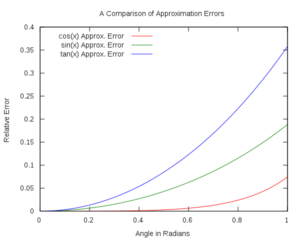
Graph (c) Phancy Physicist (CC BY-SA 3.0)
Deriving the formulas:
To actually derive the formulas for small angle approximations, the easiest method is rooted in a calculus concept called Taylor series. Using Taylor series, you can expand the trigonometric functions into a series of polynomials. This series might first appear even more complex, but by looking at the progression of polynomials, one can notice that the series decreases over time. Therefore, to simplify the formula, we can treat the latter terms as zero. Furthermore, by assuming the angle itself is extremely small, you can ignore all but the first term. Finally, that is how you arrive at the final solutions for each function.
This derivation also explains why the approximation becomes more accurate as the angle approaches zero. Since each term in the Taylor series is a polynomial function of theta, so the closer to zero the angle is, the easier it is to ignore the latter terms. The graph also shows this as the error increases exponentially when the angle increases.
I think the use of small angle approximations is incredibly useful as it allows individuals to approximate answers to incredibly complex questions. Especially in fields like physics, where different equations and calculations can grow exceptionally long extremely quickly, these approximations allow for scientists to develop a better understanding of the world to a reasonable amount of error without having to overcomplicate details. Furthermore, these formulas can shorten equations from what seems like a barely readable string of numbers and letters to an easily understandable phrase. This allows for ordinary people who may not have as much knowledge in the field to develop a reasonable understanding of the discipline itself.
Leave a Reply