In this part of my blog series on the dozenal system, I will talk about both small and large number counting in the dozenal system, and how we can still count on our hands in the dozenal system. Before you read this, I suggest checking out the first two parts of this blog series here and here.
In the first part of my blog, I talked about how the only reason that we count in tens is because of the fact that we have ten fingers. It seems very intuitive to everyone, including myself that counting the whole fingers as representative of one makes a lot of sense. As this is how we teach children how to count, we need to have another way to do this for the base 12 system.
Some more inquisitive readers might be glancing down at their hands and see that each finger is made up of 3 sections. Using your thumb to point, your four fingers multiplied by the number of sections is 12. As shown here:
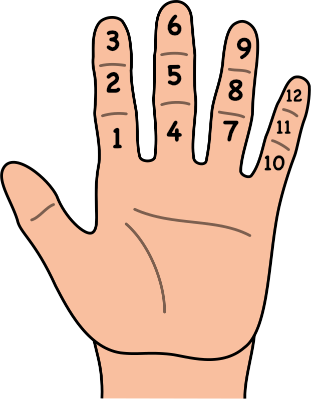
Duodecimal Fingers (c) Erik Engheim, CC BY-SA 4.0
You could then use your hand to indicate how many groups of twelve you have, and then easily count up to 144, which is large enough to work with for teaching children. And, greater than the 10 that our base ten system allows for.
In this respect, dozenal works as well for the small number counting that we teach children as decimal, and arguably better. When we start to deal with multiple digit places, it is obvious that like the decimal places, we need names for all of the places.
For decimal we would read the number 941,375,862 as nine hundred forty-one million, three hundred seventy-five thousand, eight hundred and sixty-two. The purpose of the names like million, hundred and the -ty suffix is to indicate the position of the numbers. Dozenalists don’t use the same names, because they sound too much like base 10, and have come up with their own list, and how to pronounce them.
Dozenalists use the names dozen, grosan, monan, dozen monan, grosan monan, bian, dozen bian, grosan bian, thrian and so on. In dozenal, the decmial number 941,375,862 would be written 223,321,846 and pronounced two grosan two dozen 3 bian, 3 grosan 2 dozen 1 monan, 8 grosan 4 dozen six.
I have to admit, when i was reading about these names, they all seemed abstract and bizzare to me, but, as i read more about them, i realized how bizzare and abstract hundreds and tens are, it is only by use that they become normal to us.
In the next and final part of my blog series on the dozenal system, I will talk about the time we almost ended up using the dozenal system, and why unfortunately, we likely never will.
Leave a Reply