Infinity

Symbol of Infinity. CC BY-SA 3.O
Infinity is a concept that has always fascinated me. It’s a rather simple idea that arises when you think about numbers. As a kid, I remember thinking about what the largest number would be. I realized quite quickly that you can always add one to the largest number you can think of- and get an even larger number!
You can do that process an infinite amount of times!
But as I started to delve deeper into mathematics, infinity became even more fascinating.
There are different types of infinity. Although, not all of them are the same size. Some are bigger than the others. You might be wondering, how is this possible!? Infinity goes on forever. Infinity can’t be larger than another infinity!?
Well, let’s start off with an example with natural numbers and perfect square numbers.
Natural Numbers
Are there more natural numbers (1,2,3,4 etc), or are there more perfect square numbers (1,4,9,16 etc)?
If you guessed that there are more natural numbers. Congratulations, your wrong! But let me explain.
You might be thinking that perfect square numbers occur less than natural numbers so there must be more natural numbers. For example, between 1 and 9, there are 9 natural numbers but only 3 perfect squares. However, this reasoning doesn’t account for the fact that the sets (a collection of objects) of natural numbers and perfect squares are infinite.
Think about it this way. If you were to give me any natural number. I will be able to give you the square of that number. In other words, if you give me a number from the set of natural numbers. I will be able to give you a number from the set of perfect squares that corresponds to that natural number. If you give me 1, I will give you 1, you give me 2, I’ll give you 4 , if you give me 3, I’ll give you 9, if you give me 4, I’ll give you 16 and so on.
Every natural number corresponds to a perfect square. This is called one-on-one correspondence. Which means that the amount of natural numbers is equal to the number of perfect squares. The 2 “infinities” are equal in size.
Countable Infinity
Countable infinity is a term used to describe an infinite set when you can correspond every element in that infinite set with a natural number. This means that you will be able to list every element in that infinite set. You might be thinking, wouldn’t that take an infinite amount of time? Yes, but you would be able to list off a particular element in a finite time.
Consider the previous example. By corresponding the natural numbers to the set of perfect square numbers you would be able to list and account for all perfect squares. So eventually, you will reach 1.5241579* 10^16 which is the square of 123456789 and so on.
Let’s take the set of integers as an example: [0,1,-1,2,-2,3,-3…]. It might appear as if the set of integers is bigger than the set of natural numbers because they seem to have “double” the numbers. However, once again, that reasoning doesn’t consider that both sets are infinite. You can actually correspond every natural number with an integer. 1 with 0, 2 with 1, 3 with -1, 4 with -2 etc. This means that both sets are equal in size. For example, in a finite set of time you will be able to account for the integer -488286489274623462 because it would correspond to a natural number.
All infinite sets that can be classified as countable infinity are equal in size.
Uncountable Infinity
Uncountable infinity is a more difficult term to wrap your head around. The term uncountable infinity is given to an infinite set when every element in that set cannot correspond to a natural number.
The set of all real numbers is uncountable. You might be wonder how that’s possible. Aren’t you able to list all the decimals, fractions and irrational numbers? Well, we can try that, let’s try to list all the decimals going infinitely down and to the right.
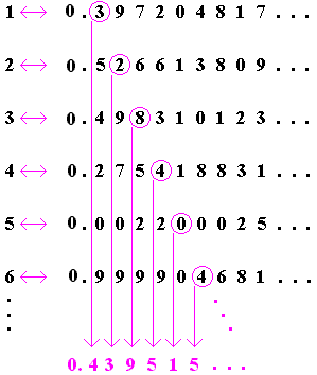
List of decimals proving that they are uncountable. CC BY -SA 3.0
In the image above, a bunch of decimals are written to the right and they go on forever. They also go downwards forever. So, you can try to correspond every decimal with a natural number. However, I will always be able to give you a decimal that will not be on your list.
I will do that by taking digits from each decimal diagonally. So, the decimal I will get is 0.328404… Now, what I will add 1 to every digit in the decimal, and if the digit is a 9 I will replace it with a 0. So my new decimal is 0.439515…
I’ve created this new decimal and it is not going to be on that original list of decimals. Simply changing the digit for each place in the decimal will ensure, that the new decimal is not going to be on any list of decimals you come up with. How does this work?
Ok, if I wanted to get a decimal that will be different than the first decimal on the list, I just have to make sure that the first digit of my decimal is different than the first digit of the decimal on the list. This will ensure that my decimal will be different than the first decimal. Then if I wanted to ensure that my decimal is different than the second decimal on the list, I just have to make sure that the second digit of my decimal is different then the second digit of the second decimal on the list. If I wanted to make my decimal different than the third decimal on the list, I just have to make sure that the third digit of my decimal is different than the third digit of the third decimal on the list.
See how if the list went on forever, I’m still able to ensure that my new decimal will always be different than all of the decimals on the list. Furthermore, you are trying to correspond a natural number to each decimal. But I just gave you a decimal that wasn’t on the list and I can still give you infinitely more decimals that you won’t be able to account for.
This means that you cannot correspond a natural number to all of the decimals/real numbers. From this, you can deduce that the set of decimals/real numbers is larger than the set of natural numbers.
Also, since you cannot list or count all of the decimals/real numbers it is called uncountable infinity.
Uncountable infinity is larger than countable infinity.
Georg Cantor
These concepts surrounding infinity were created by mathematician Georg Cantor (1845-1918). At his time, his work was heavily criticized. People thought he was crazy. In fact, later on in his life, he would spend time in a mental asylum which would also be his place of death.

Picture of Georg Cantor CC BY-SA 3.0
People just thought his work made no sense. How could one infinity be bigger than the other? How can you count and not count infinity? These questions and especially Cantor’s answers puzzled mathematicians and they just didn’t like the logic revolving around infinity that Cantor used. However, later on in his life and after he died people realized the significance of his work and understood that the logic he used was correct.
Infinity is a very difficult concept to grasp but I find it amazing and fun to play around with. I was really surprised when I first learned these topics and was doubtful of the logic. But in order to really comprehend it, you have to sit down and let go of common sense to really get an intuitive understanding and appreciation of infinity.
Leave a Reply